Home >>DBMS Tutorial >DBMS Indexing
DBMS Indexing
DBMS Indexing
We know that data in the form of records is stored. There is a main field in any record, which allows it to be recognized uniquely.
Indexing is a data structure technique based on certain attributes on which the indexing has been performed to efficiently extract information from database files. In database systems, indexing is close to what we see in books.
Based on its indexing attributes, indexing is specified. Indexing can be of the types below-
- Primary index − − The primary index in an ordered data file is specified. In a key field, the data file is ordered. The main area is normally the relations primary key.
- Secondary index -Secondary index can be created from a field that is a candidate key and in every record has a unique value, or a duplicate value non-key.
- Clustering Index- In an ordered data file, the clustering index is specified. A non-key field is ordered by the data file.
Ordered Indexing is of two types −
- Dense Index
- Sparse Index
Dense Index
In the dense index, for every key search value in the database, there is an index record. This makes searching quicker, but requires more space for index records to be stored on their own. Index records contain the value of the search key and a pointer to an actual disk record.
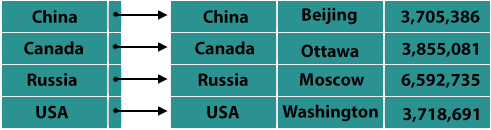
Sparse Index
Index records are not generated for each search key in the Sparse Index. There is a search key and an actual pointer to the data on the disk in an index record here. We first proceed to an index record to search for a record and reach the actual location of the data. If the data we are looking for is not where we reach directly by following the index, then before the desired data is found, the system starts sequential searching.
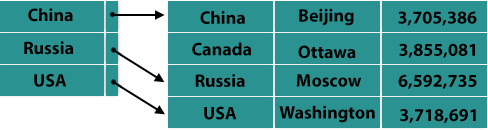
Multilevel Index
Search-key values and data pointers comprise the index records. The multilevel index, along with the individual database files, is stored on the disk. As the database's size increases, so does the indices' size. In order to speed up the search operations, there is an immense need to retain the index records in the main memory. If a single-level index is used, it is difficult to hold a broad index in memory, which leads to multiple accesses to the disk.
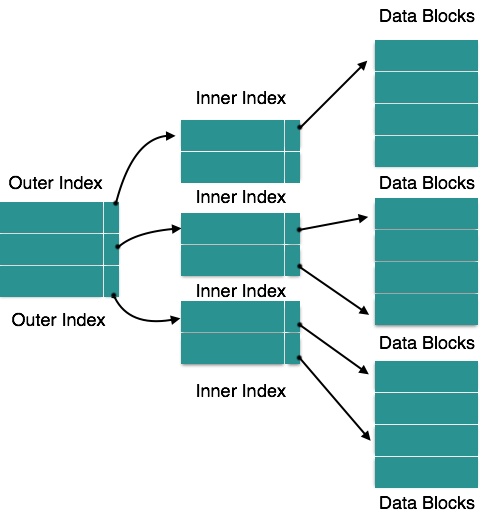
In order to make the outermost level so small that it can be stored in a single disc block, which can easily be accommodated anywhere in the main memory, the multi-level index helps break down the index into many smaller indices.
B+ Tree
A B+ tree follows a multi-level index format and is a balanced binary search tree. A B+ tree's leaf nodes denote actual data pointers. The B+ tree ensures that all leaf nodes stay balanced at the same height. In addition, a link list connects the leaf nodes; a B+ tree can therefore allow both random access and sequential access.
Structure of B+ Tree
Each node on the leaf is the same distance from the root node. For any B+ tree, a B+ tree is of the order n where n is fixed.

Internal nodes −
- Internal (non-leaf) nodes, except the root node, contain at least of [ n/2 ] pointers
- At most, n pointers may contain an internal nod
Leaf nodes −
- At least [ n/2 ] record pointers and [n/2] key values are stored in Leaf nodes.
- At most, n record pointers and n key values will contain a leaf node.
- Each node of the leaf contains a block pointer P to point to the next node of the leaf and forms a linked list.
B+ Tree Insertion
- From the bottom, B+ trees are filled and every entry is done at the leaf node.
- If a leaf node overflows −
- Split node into two parts.
- Partition at i = ⌊(m+1)/2⌋.
- First i entries are stored in one node.
- Rest of the entries (i+1 onwards) are moved to a new node.
- ith key is duplicated at the parent of the leaf.
- if a non-leaf node overflows −
- Split node into two parts.
- Partition the node at i = ⌈(m+1)/2⌉.
- Entries up to i are kept in one node.
- Rest of the entries are moved to a new node.
B+ Tree Deletion
- At the leaf nodes, B+ tree entries are deleted.
- The entry for the goal is searched and deleted.
- If it is an internal node, delete it from the left position and replace it with an entry.
- The underflow is tested after deletion,
- If there is an underflow, allocate the entries from the nodes left over.
- If distribution from the left is not possible, then
- Distributing right to it from the nodes.
- If distribution from the left or from the right is not feasible, then
- Merge to the left and right of the node.
